【人気ダウンロード！】 sin 面積 287275

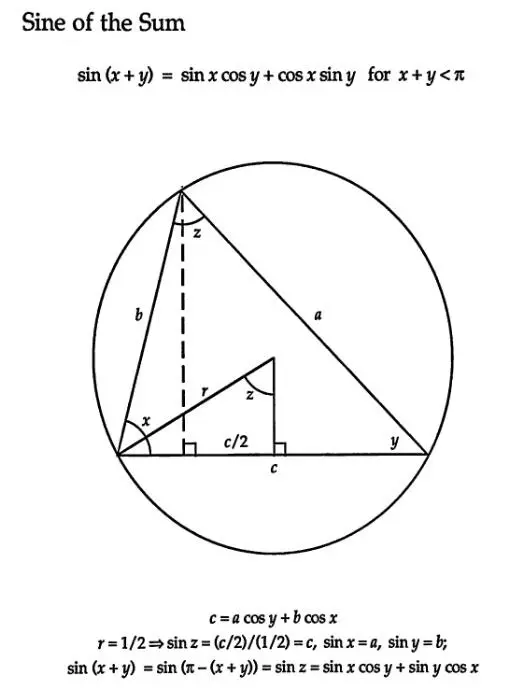
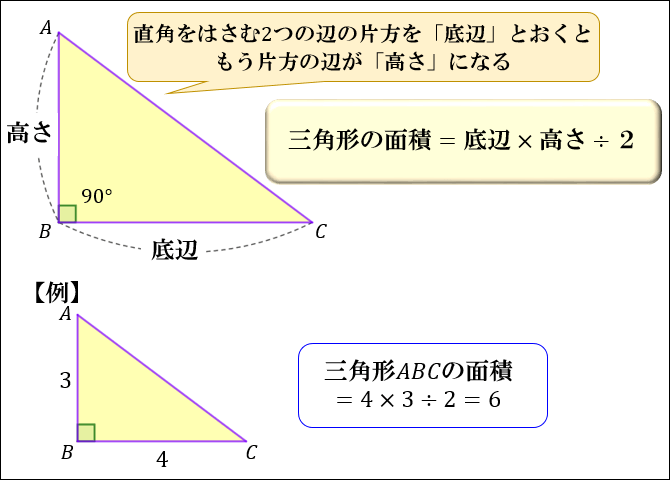
積分 sinθ の図形による理解 ∫ sinθdθ ∫ sin ⁡ θ d θ の積分を図形を用いて直感的に理解する． 左側の図は 単位円 ，右側の図は y =sinθ y = sin ⁡ θ のグラフである． 図において赤色の面積と青色の面積は等しい． ∫ π 2 0 sinθdθ =−cosθπ 2 0 = −cos π 21 sin2 cos d = 2 2 0 cos2 d = 2 0 (1 cos 2)d = 2 D dS は領域 の面積であることに注意．D この場合は半径1の半円の面積だから明らかに 2 丸いものを四角く計算していてセンスが悪い． 丸いものは丸く三角形の2辺と角度（°）を入力 辺 a = 3 辺 b = 4 角度（°）= 30 面積 S = 3000 三角形の2辺と角度（°）を入力 辺 a = 54 辺 b = 126 角度（°）= 58 面積 S = 251 このように三角形の面積を計算してみました。 その他のサンプルプログラムも合わせてご覧ください

无字证明 第8期 三角函数与三角学篇 哔哩哔哩

Sin 面積

Sin 面積- 4 三角比の面積公式 三角比を使って、三角形の面積を求める公式です。 公式が成り立つ理由や詳しい解説は「数学Ⅰ三角比sin cos tanの面積公式と覚え方」の記事でまとめているので、ぜひ参考にしてください。 y=sin(x)(0≦x≦2π)とx軸とで囲む面積。計算途中と答え教えてください。お願いします。 数学 解決済 教えて！goo

三角形面积公式sin 万图壁纸网

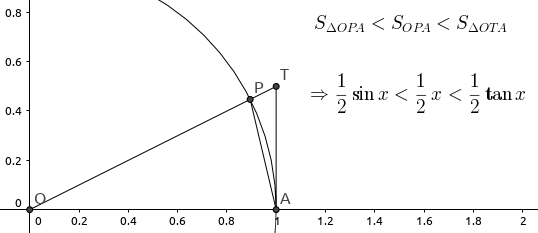
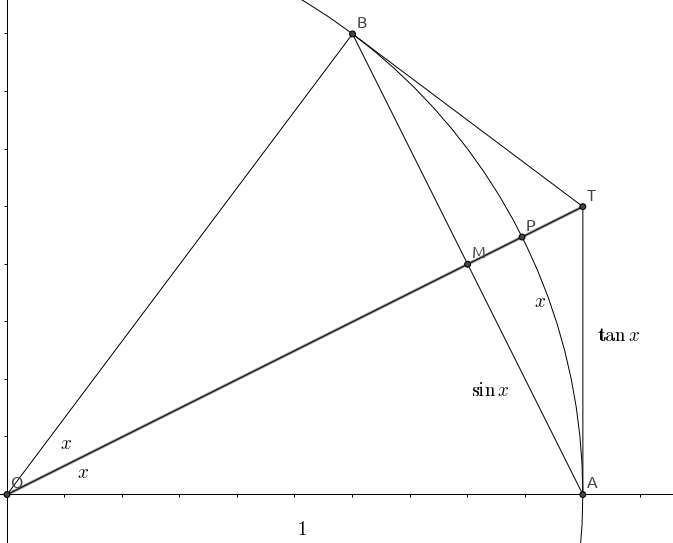
面積は厳密には積分によって定義さ れる。この場合は扇形の面積が問題であるが、それは三角関数の積分に帰着し、積分の計算には三角関数の微 分を用いることになる。ところがlimx!0 sinx x = 1 はsinx のx = 0 における微分係数が1である、という主極限 x →0 sin x / x lim x→0 sinx x = 1 lim x → 0 sin x x = 1 の関係を導く． となる．直感的に，この値は1より小さい値であるとわかる． 予備知識として，弧EF（ xcosx x cos x ），DE（ sinx sin x ），弧BD（ x x ），BC（ tanx tan x ）の長さの関係を導いておくことに1 第1章 三角関数の極限と近似 三角関数の極限 ⃝1 lim →0 sin = 1 ···(基本公式) ⃝2 lim →0 1−cos 2 = 1 2 ···(準公式) x y O A(1;0) P T H 証明単位円上に，中心角が (単位はラジアンで;

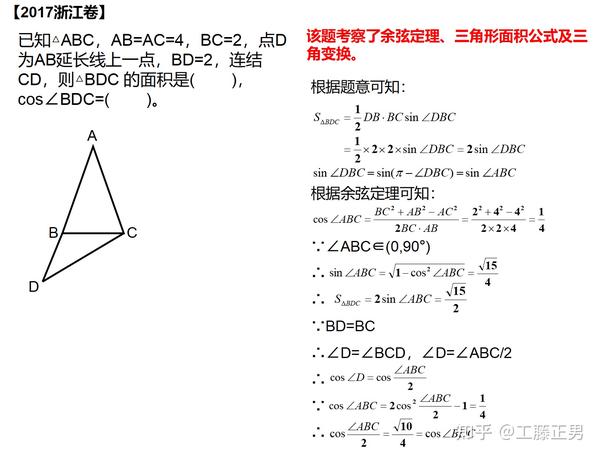
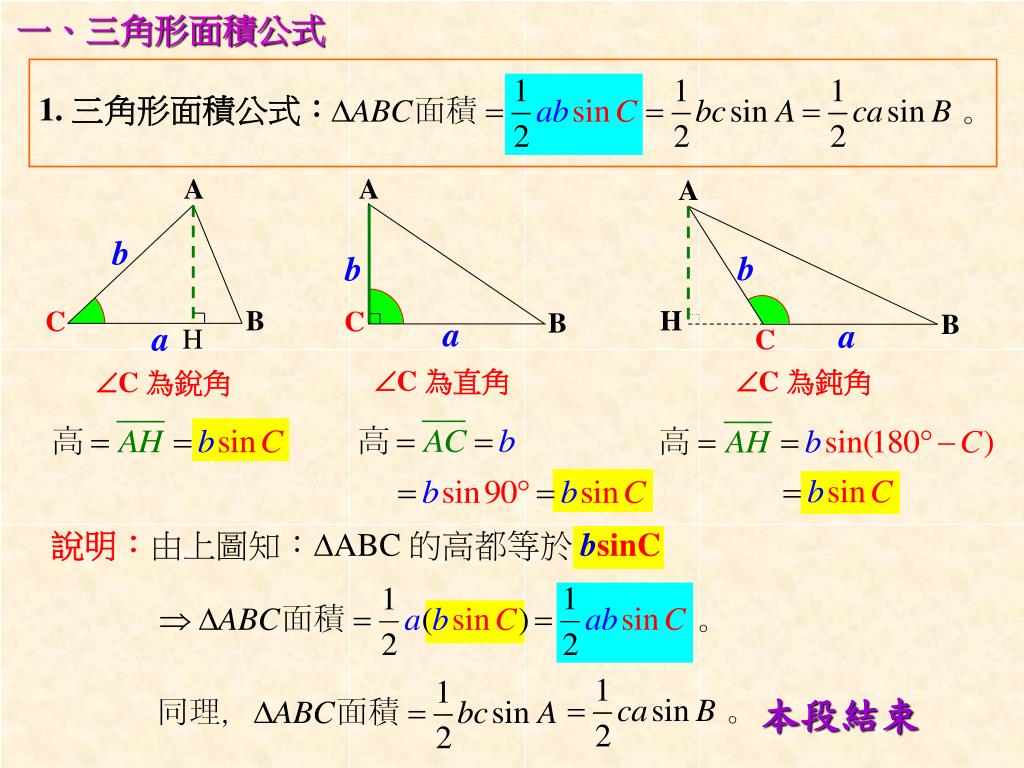
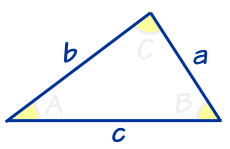
四角形の2本の対角線の長さを a, b 対角線の交わる角度を θ としたとき、四角形の面積 S は、 S = 1 2 a b sin ⁡ θ 式B である。 ことが分かる。 ということで、問題を解こう。 式Bより、問題の四角形の面積 S は、 S = 1 2 ⋅ 5 ⋅ 4 sin こういう場合には、面積公式に必要な\(\sin\)の値を求めることからスタートします。 とは言っても、いきなり\(\sin\) の値を求めることは難しいので一旦、\(\cos\) の値を求める。 その後、\(\sin\) に変換するといった流れでやっていきます。定理《三角形の面積》 A B C \triangle\mathrm {ABC} ABC の面積 S S S は, S = 1 2 b c sin ⁡ A = 1 2 c a sin ⁡ B = 1 2 a b sin ⁡ C S = \frac {1} {2}bc\sin A = \frac {1} {2}ca\sin B = \frac {1} {2}ab\sin C S = 21

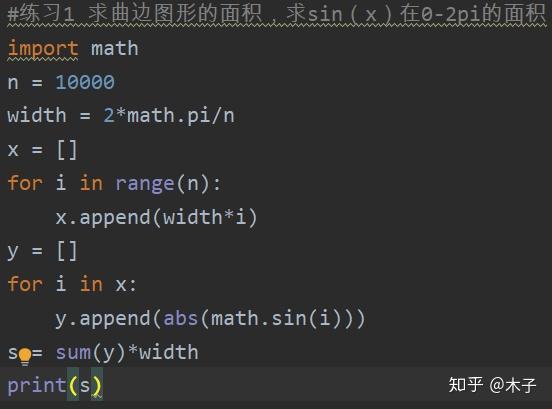
心臟線 維基百科，自由的百科全書 跳至導覽 跳至搜尋 心臟線 一個圓滾動產生的心臟線 使用圓和切線生成一個心臟線 心臟線 是有一個 尖點 的 外擺線 。 也就是說，一個圓沿著另一個半徑相同的圓滾動時，圓上一點的 軌跡 就是心臟線。 曼德博集合 中間都道府県別スギ・ヒノキ人工林面積 北海道 5,542,533 32,571 0 1 青森 634,785 1,036 108 32 岩手 1,172,463 2,871 3,996 18 宮城 417,924 134,050各長方形の幅は01πです。高さはsin(theta)です。 よって、=01**d4を計算して、 各段についても計算します。(長方形の数はsinの計算より一つ少ない） これが各長方形の面積です。求めたい積分はこれの合計なので、合計してみます。 結果はでした。

三角函数小题 解三角形专题 知乎

求两圆相交的公共面积 Excel如何求两圆相交部分的面积 三人行教育网 Www 3rxing Org

例えば面積 S=1/2*()^2*(sin())= 弓形の半径と中心角から弓形の面積、円弧の長さ、弦の長さを計算します。正弦波とは波源が単振動をすることで, sin もしくは cos の関数に従う位置の変化が周りに伝搬する x 方向へ速さ v で進む正弦波は下図のようになる x 方向に対して垂直な方向への媒質の変化を 変位 という 最大変位 A を 振幅 という 正弦波において sin = 高さ / 斜辺 例えば、底辺と斜辺の角度が30°の直角三角形の場合、高さは1で斜辺は2になるのでsin30の値は以下のよう表すことが可能です。 sin30 = 1 / 2 = 05 sin関数の使い方 Math関数にあるsin関数は以下のように使いましょう。

高校 数学i 図形と計量 三角形の面積sinの利用 Youtube

定积分求y1 Sin5x与y2 Sin7x围成的面积 百度经验

上図において正弦波の式は、 \begin{eqnarray} v(t)=V_M\sin{{\omega}t} \end{eqnarray} で表すことができます。 上式を用いると、正弦波の実効値・平均値・波形率・波高率を求めることができます。数学Ⅱ（三角関数）：円弧の長さと扇形の面積（弧度法） 対象 高2 再生時間 328 説明文・要約 〔半径 r、中心角 θ（ラジアン）の扇形について〕 ・円弧の長さは rθ 円周の長さ 2πr に対して、中心角の割合が θ/2π であるため もしくは右の表2は，定積分 sin x dx の値を100 台形の面積は（上底下底）×高さ÷2で求められますが，この上底を左端の縦の長さに当てはめ，下底を右端の縦の長さに，高さを横幅に当てはめると，例え

四邊形面積 Wonder Math

高考数学考点之正 余弦定理及解三角形 王羽课堂

サイン (sin)を使った三角形の面積を求める公式とその証明 三角形の面積を求める公式といえば「 底辺×高さ÷2 」を思い出しますが、ここでは「サインを使って三角形の面積を求める公式」を紹介します。 ではこの公式を証明していきましょう。 図のよう0 < < ˇ 2) の扇形OAP を考え, P からx 軸に下ろした垂線の足をH，A にお ける接線と半直線OP の交点をT とすると，二辺と挟まれる角が分かっている場合は、面積を求める公式を用いる 二辺a、bとその二辺に挟まれた角Aが与えられた時、面積(A)＝1/2ab(sin C)が成り立ちます。Aに三角形の面積の公式をあてはめると、1/2bh = 1/2ab(sin C)となります。

三角形的面積

三角函數

円弧面積の計算式 扇形面積＝円の面積×（ 扇の内角／360°） 三角形の面積＝（ 半径 2 扇の面積－三角形の面積＝円弧の面積 WingneoのIAの計算方法 円弧の始点・終点2点の座標値を丸める。「円弧面積の弦長を求める為の座標丸め」 その2点間距離を求めるあとは、 サインを使って三角形の面積を求める公式 より ・ サイン (sin)を使った三角形の面積を求める公式とその証明 ・ 直方体を切り取った図形の面積 ・ 三角比を使って円に内接する四角形の辺の長さ、面積を求める方法 ・ 三角比で三角形の面積を1 0 であるから，「はさみうちの原理」より(sinx)=x !

面積公式sin Ookkk3 Nnsaru

三角形心系列 外心篇 三角形外心及其面积公式 哔哩哔哩 Bilibili

1． どこが問題なのか？一見何の問題もないように見えるが， (a) 平面図形の「面積」の定義が明確に定義できているか？ (b) その上で，「三角形の面積」，「扇型の面積」が正アステロイド曲線は媒介変数 θ \theta θ を用いて x = a cos ⁡ 3 θ, y = a sin ⁡ 3 θ x=a\cos^3 \theta, y=a\sin^3\theta x = acos3 θ,y = asin3θ と表すことができます。 アステロイド曲線は，半径 a a a のSin q ， cos q の 0 から p / 2 までの定積分すなわち面積は である．そして， cos q は sin q を p / 2 平行移動したものでありかつ周期関数である．この性質を理解すれば角度 0 から， n p /2 ： n は整数，の定積分値が簡単にわかる．

三角形面积计算公式 三角形面积计算的万能公式 52fmz购物网

三角形面积用sin表示 三角形的面积公式sin 解三角形三角形面积

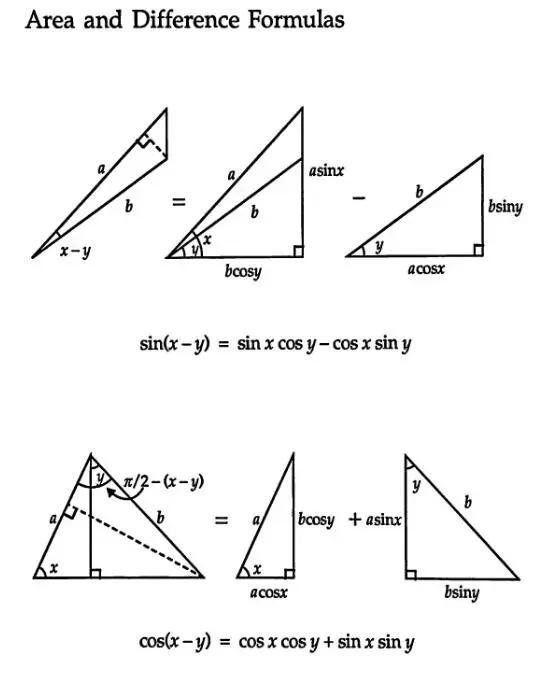
B\sin C bsinC となるため、 A B C ABC ABC の面積が求められます。 図 2 A B C a b c b sin C A B C の 面 積 = a b sin ⁡ C 2 ( 3) ABC\text { の面積}=\frac {ab\sin C}2 \tag {3} ABC の面積 = 2absinC (3) 同様に他の 2 辺とその間の角から面積が求められます。Sinを用いる三角形の面積公式 証明 sinを用いた面積公式の証明をしておきましょう。 三角形ABCにおいて、角Cから辺ABに垂線を引き、垂線と辺ABの交点をHとする。 すると ACHができる。 なので、 三角形の面積は 「底辺×高さ÷2」 でしたね。 したがってこの公式自体に三角関数は現れませんが、上の sin を用いた面積公式と、余弦定理から導かれています。 2直線のなす角と傾きの関係 2直線の傾きとその間の角 θ に関して、次の式が成り立ちます。

无字证明 第8期 三角函数与三角学篇 哔哩哔哩

高中数学牛x 公式 利用平面向量快速求三角形面积 1 努力学习网

 このページは、このような人へ向けた内容となっています 三角比を使った三角形の面積の求め方を知りたい 三角比の公式は知っているが使い方がわからない 三角形の面積を求めるための、色々な方法を知りたい 三角比（\\(\\sin, \\cos, \\tan\\)）を使った三角形の面積を求める方法はいく2 であるから， sinx 2 < x 2 < tanx 2 cosx < sinx x < 1 x !Step 2 cos Aから，sin Aを求める。 ここで，Aの大きさはわかりませんが，面積を求めるためにはAの大きさがわからなくてもsinAの値がわかれば十分なのです。 ★これで，公式 を使う準備ができました。あとは，面積の公式に当てはめるだけです！

利用正弦計算三角形面積 Finding Area Of A Triangle By Sine Ratio Youtube

數學 高二上三角函數公式 小編過路君子

正弦定理三角形面积公式 扒拉扒拉

高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト

三角形的面积公式 腾讯视频

腾讯视频

三角函数 玄数

三角形面积公式直观证明高考数学考研数学基础知识 哔哩哔哩 つロ干杯 Bilibili

三角形面积公式 三角形面积公式盘点 52fmz购物网

正弦定理的常见变形

數學 高二上三角函數公式 小編過路君子

土气和洋气的方法不用p求圆的面积 Netfilter Iptables Openvpn Tcp Guard Csdn博客

三角形面积公式sin计算公式推导过程详解说明 小街网

无字证明 第8期 三角函数与三角学篇 哔哩哔哩

Ch07 三角學19 單元測驗 05 任意三角形面積 Youtube

三角形面積公式sin 三角形面積公式 Duph

Knowledge Teaching 圓形 缺角圓形面積計算 Area Calculation Of Circle Cutting Area Circle

数理之路 三角形面积公式以及三角函数正弦和角公式 腾讯新闻

三角形面积公式sin 冷知识 球面三角形面积是怎样求出来 尚书坊

Ppt C 為直角powerpoint Presentation Free Download Id

三角形面积公式 搜狗图片搜索

三角形面積公式 兩邊一夾角 Youtube

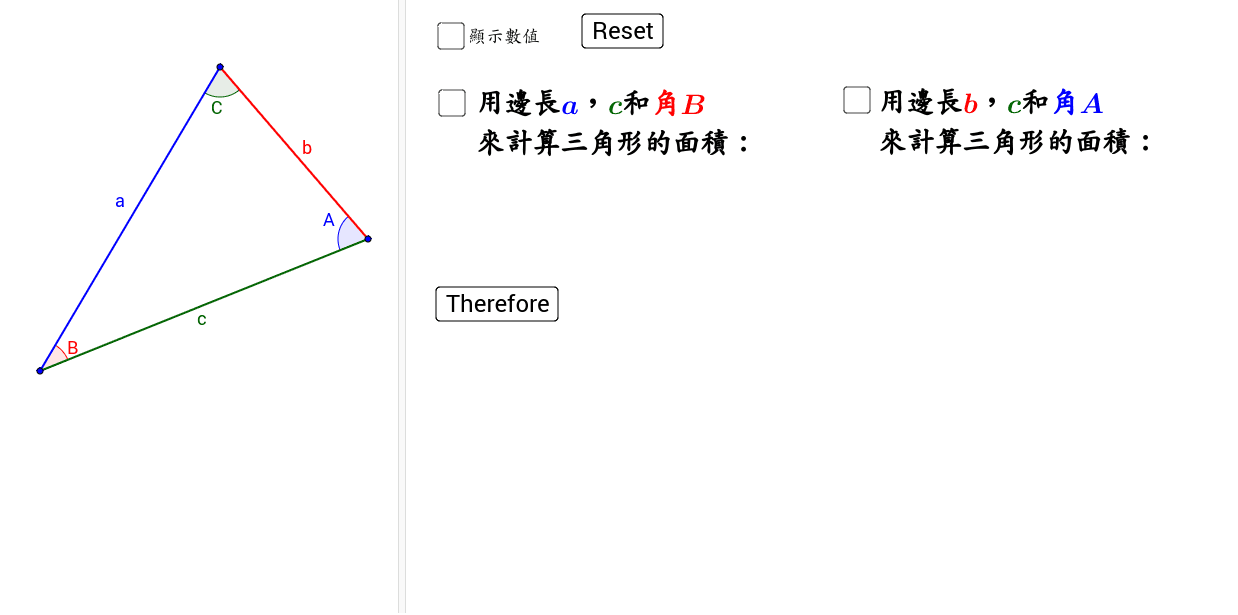
Proof Of Sin Formula正弦公式的證明 Geogebra

三角形面积公式 腾讯视频

三角形的面積

菱形面积公式 快懂百科

三角面积公式sin是多少 扒拉扒拉

3 10 三角形面積公式的推導 Youtube

余弦定理求三角形面积公式 高三网

等边三角形面积如何计算等边三角形面积怎么计算

Sinを用いた三角形の面積公式 高校数学の美しい物語

三角形面积的计算公式 Sumyblog

只要三张图 轻松帮你搞定三角形面积的17种求法

三角形面积公式sin 万图壁纸网

程俊老師 三角形面積公式整理 Facebook

學測數學98填i Sas求面積 配合算幾不等式 數學 均一教育平台

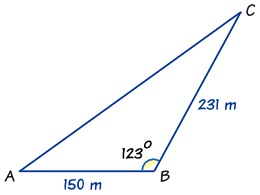
非直角三角形的面积

三角函数是必考题 如何学会 先把这块基础抓好

圆扇形与弓形

三角形面积公式 搜狗图片搜索

初中数学 函数几何综合常见题目 求三角形面积 腾讯视频

トップ100 正三角形面積小学生 最高のカラーリングのアイデア

Sin Cos Tan 系列３ 求三角形面積嘅時候用底乘高除二大家就聽得多啦 但係如果用另一條公式用sin大家又聽過未呢

1

数理之路 三角形面积公式以及三角函数正弦和角公式 腾讯新闻

三角形面積公式 正弦 引入 Youtube

三角形的面積

高中數學 三角函數 正弦定理與餘弦定理 1 三角形面積公式 吳汀菱 Youtube

三角形的面积公式十叙 知乎

Amc10 数学中的面积公式推证

Sin平方角公式 西瓜视频搜索

对面积的曲面积分 Jason S Blog

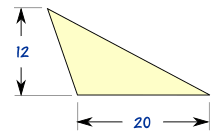
非直角三角形的面积

Sinを用いた三角形の面積公式 高校数学の美しい物語

1

三角形面积公式推导 万图壁纸网

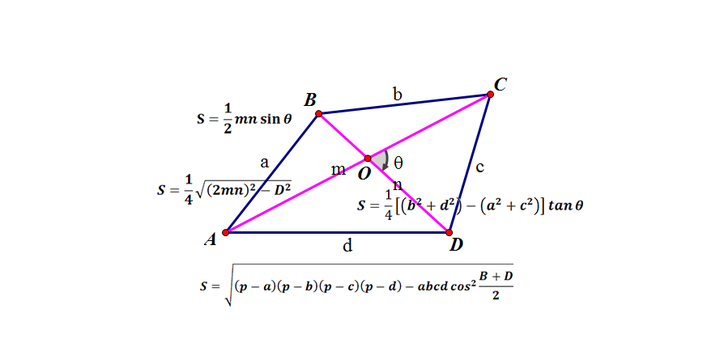
四边形的面积公式 知乎

三角形的面積

正弦区域高度面积公式的三角形律png图片素材免费下载 图片编号 Png素材网

关于python 计算四边形的面积 码农家园

數學 高二上三角函數公式 小編過路君子

余弦定理求三角形面积公式 高三网

三角形面积公式 腾讯视频

解三角形中求面积最值 利用积化和差化简技巧 每日头条

三角形的面积 视频在线观看 爱奇艺搜索

三角形的面積

非直角三角形的面积

少有人走的路 三角函数超入门 4 钝角三角比 三角形面积

三角形邊長公式

椭圆面积公式 搜狗百科

三角形外接圆面积公式 搜狗图片搜索

正在計算界定面積

怎么计算三角形面积 生活百科

教學0 5absinc Heron Formula Sine Cosine Formula 三角形面積公式 希羅公式 正弦及餘弦定理 Youtube

圆的面积凭什么是pr Li Hua 博客园

初中数学 求三角形的面积 初中生求不了22 5度的正余弦 咋办 哔哩哔哩 つロ干杯 Bilibili

几何直觉的魅力 Sinx曲线下的面积原理是如此的美妙 正弦 圆周 斜边 三角形 网易订阅

三角形面积公式例题 搜狗图片搜索

淺談 三角形面積公式 Hackmd

圆的面积凭什么是pr Li Hua 博客园

国际数学竞赛 三角形面积公式知多少 知乎

计算凸多边形的面积 Qq 的博客 程序员宅基地 程序员宅基地

十七种三角形面积公式

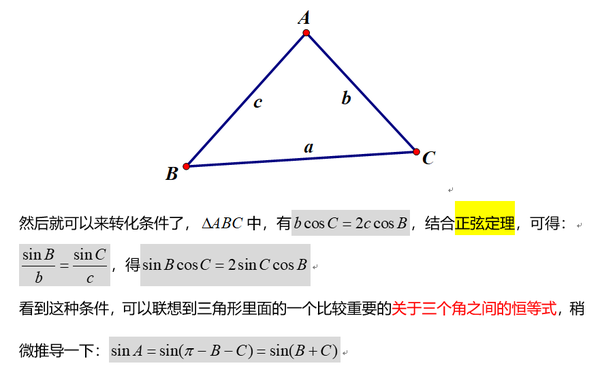
呆哥数学每日一题 求三角形面积最大值 知乎

温故知新 三角形面积公式新求法 腾讯视频

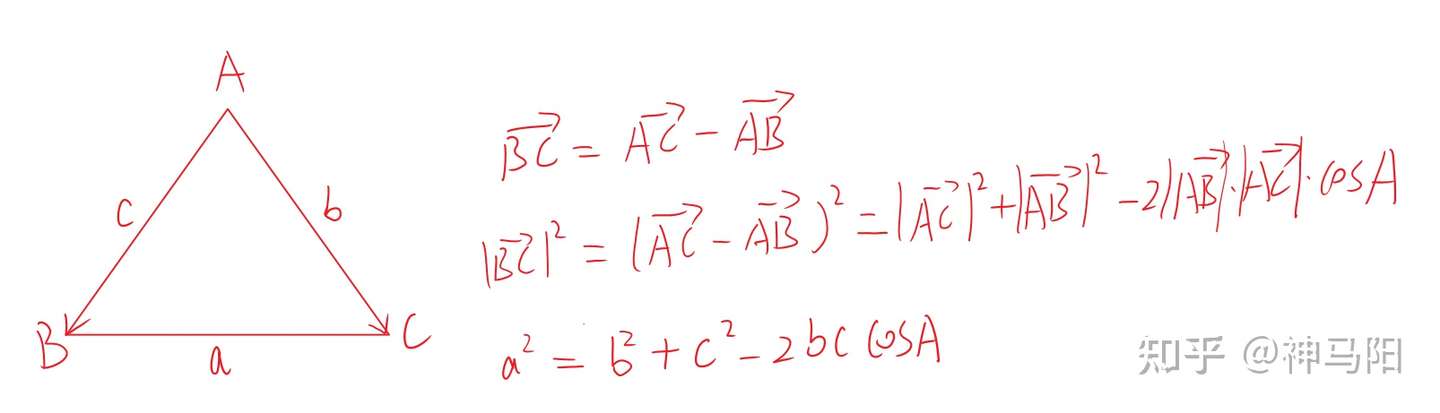
解三角形 知乎

Section 2 2 P2 8 Evaluation Of A Closed Surface Chegg Com

為什麼aob面積要乘以sin1度 Clearnote